CMU15-445 PROJECT2 B+TREE INDEX 项目记录

Checkpoint1 Single Thread B+Tree

B_PLUS_TREE_PAGE

Task1 的实现非常简单，都是一些普通的 Getter 和 Setter。

首先更深入了解以下Page的含义。Page.h中关于Page的成员定义如下：

1
2
3
4
5
6
7
8
9
10
/** The actual data that is stored within a page. */
char data_[BUSTUB_PAGE_SIZE]{};
/** The ID of this page. */
page_id_t page_id_ = INVALID_PAGE_ID;
/** The pin count of this page. */
int pin_count_ = 0;
/** True if the page is dirty, i.e. it is different from its corresponding page on disk. */
bool is_dirty_ = false;
/** Page latch. */
ReaderWriterLatch rwlatch_;

其中，data_ 是实际存放 page 数据的地方，大小为 BUSTUB_PAGE_SIZE，为 4KB。其他的成员是 page 的 metadata。

B_PLUS_TREE_PAGE插入

b_plus_tree_page 是另外两个 page 的父类。有以下私有成员：

1
2
3
4
5
6
IndexPageType page_type_;
lsn_t lsn_;
int size_;
int max_size_;
page_id_t parent_page_id_;
page_id_t page_id_;

B_PLUS_TREE_INTERNAL_PAGE

b_plus_tree_internal_page对应 B+ 树中的内部节点。不同的是，他有以下这个私有变量：

1
MappingType array_[1];

internal page 中没有新的 metadata。这里是一种特殊写法，叫flexible array。

在C++中，flexible array是指在结构体的最后一个成员位置定义一个未知大小的数组，这个数组不占用结构体的空间，只有在分配内存时才会为其分配空间。这里的 array[1] 利用 flexible array 的特性来自动填充 page data 4KB 减掉 header 24byte 后剩余的内存。剩下的这些内存用来存放 KV 对。

internal page 中，KV 对的 K 是能够比较大小的索引，V 是 page id，用来指向下一层的节点。

这里有个问题，项目要求一个 Key 为空，这是为什么呢？ > 主要是因为在 internal page 中，n 个 Key 可以将数轴划分为 n+1 个区域，也就对应着 n+1 个 value，则需要有一个key是空的，这里就统一为第一个Key为空就行了。

B_PLUS_TREE_LEAF_PAGE

leaf page 多了一个成员变量next_page_id，指向下一个 leaf page，所以前面#define LEAF_PAGE_HEADER_SIZE 28。插入ecord id 用于识别表中的某一条数据。leaf page 的 KV 对是一一对应的，不像 internal page 的 value 多一个。 这边主要有三个任务：查找GetValue()、插入Insert()、删除Remove()。

查找

查找相对来说比较简单，基本思路是 先找到key对应的叶子页面FindLeaf()，然后在这个叶子节点中找到key对应的value KeyIndex()。也就是实现这两步走。

在实现FindLeaf()时： 拿到一个 key 需要查找对应的 value ，首先需要经由 internal page 递归地向下查找，最终找到 key 所在的 leaf page。在它的一般实现中都会加入leftMost和rightMost这两个布尔参数，以便在后面迭代器的实现时找到最左边（或最右边）的叶子节点，放在这里也是因为可以顺便找到，只需要： 

1
2
3
4
5
6
7
if (leftMost) {
  child_node_page_id = i_node->ValueAt(0);
} else if (rightMost) {
  child_node_page_id = i_node->ValueAt(i_node->GetSize() - 1);
} else {
  child_node_page_id = i_node->Lookup(key, comparator_);
}

在实现KeyIndex()时，就是对二分法的一个复习，此处就不多赘述了。但二分法还是不够熟练，很多次找bug都会很不自信地去检查它，虽然没错，但就是体现出很不自信！！！

插入

  1. 如果是空树，创建一个叶节点作为根(StartNewTree)。
  2. 不管三七二十一直接插入。（这是我的做法，而且前面提到的flexible array也允许我这样做。这样还有一个好处就是，现在插入后面分裂就省心了，在这基础上split就可以，不需要再惦记这个插入了。）如果不需要split，那么到这里也就结束了。麻烦的在下面需要分裂的情况。
  3. split 创建一个新的叶节点，将原节点的一半内容拷贝到新节点(MaveHalfTo)，分裂点的键插入父节点(InsertIntoParent)，该键对应的值指向新的叶节点。如果这个时候父节点的达到了MaxSize，则需要递归分裂向上插入。

问题有蛮多的，全都放到最后一个section记录了。

在做这些最基本实现的时候，课程还提供了可视化debug方法，非常方便。在后面的问题中我也经常用到它。在解决纯算法上的问题的过程还是非常有意思的。（变相说后面的并发简直折磨人）

附上一张insert()建树图 insert测试小树

删除

一：找到目标key的叶子节点并删除键值对

调用FindLeaf()找到对应的叶子页面，然后调用KeyIndex()找到item，用叶子页面的remove操作删除之，记得更新size.

接下来，要判断一下删除后叶子页面是否到达了MinSize，没有到达的话，就可以直接return；否则就需要进行Coalesce或Redistribute操作。

二：Coalesce或Redistribute操作逻辑

  • 如果当前是根节点，则调用AdjustRoot对根节点进行处理。此时只需要更新root_page_id_为INVALID_PAGE_ID即可。

  • 然后我们需要找到它的兄弟节点，这就要先找到它的父节点。这里要选左兄弟还是右兄弟呢，其实都可以，我没有找到什么优雅的方法，就左右兄弟分别写了一遍后面的逻辑，用左兄弟的话传一个true，否则传一个false。脑子比不过人家我就勤奋一点嘛(dege)。这里就首先找到当前节点对应的index，如果index>0则说明它一定有左兄弟，那就用左兄弟；否则咱就是最左边的，只有一个右兄弟。

  • 那是用Coalesce还是Redistribute呢？判断一下：如果 

    1
    if (sibling_node->GetSize() > sibling_node->GetMinSize())
    就用Redistribute，否则合并起来就吃成胖子了这可不行。

三：Redistribute

这里主要注意一下叶子页面和内部页面的处理方式有些不同就是了。

对于叶子页面，如果从左边借（也就是说传过来的是true），那么左边好邻居给出去的得是最后那个，我得把他放在第一个，其他的往后稍稍；反之亦然，便不赘述。

然后再把父节点对应index的key更新一下。

对于内部页面，借完之后还得更新一下借来那家伙的子节点的父节点。你现在换了个爹辣！

更具体的，用代码语言描述，就是前面说的如果是叶子页面从左边借的情况（也就是说传过来的是true）： 

1
2
neighbor_leaf_node->MoveLastToFrontOf(leaf_node);
parent->SetKeyAt(index, leaf_node->KeyAt(0));

四：Coalesce

这里也要注意叶子页面和内部页面的不同处理方式。

对于叶子页面，将后面节点的全部item移到前面的节点即可。然后父节点remove对应index的item。

1
2
3
auto *leaf_node = reinterpret_cast<LeafPage *>(node);
auto *prev_leaf_node = reinterpret_cast<LeafPage *>(neighbor_node);
leaf_node->MoveAllTo(prev_leaf_node);

对于内部页面，MoveAllTo()函数中还需要注意更新孩子节点的父节点pageid。

这里贴一下CopyNFrom()函数，在所有与Move相关的函数中经常用到，这里以内部节点的版本作为示例。

1
2
3
4
5
6
7
8
9
10
11
12
13
INDEX_TEMPLATE_ARGUMENTS
void B_PLUS_TREE_INTERNAL_PAGE_TYPE::CopyNFrom(MappingType *items, int size, BufferPoolManager *buffer_pool_manager) {
  std::copy(items, items + size, array_ + GetSize());

  for (int i = 0; i < size; i++) {
    auto page = buffer_pool_manager->FetchPage(ValueAt(i + GetSize()));
    auto *node = reinterpret_cast<BPlusTreePage *>(page->GetData());
    node->SetParentPageId(GetPageId());
    buffer_pool_manager->UnpinPage(page->GetPageId(), true);
  }

  IncreaseSize(size);
}

最后因为合并了，需要向上递归，即： 

1
return CoalesceOrRedistribute(parent, transaction);

到最后，无论是合并还是往旁边借，都需要unpin一下。

1
2
3
buffer_pool_manager_->UnpinPage(parent_page->GetPageId(), true);
sibling_page->WUnlatch();
buffer_pool_manager_->UnpinPage(sibling_page->GetPageId(), true);

Checkpoint2 Multi Thread B+Tree

Index Iterator

我在实现时用了以下这些私有成员： 

1
2
3
4
5
6
private:
 // add your own private member variables here
 BufferPoolManager *buffer_pool_manager_;
 Page *page_;
 LeafPage *leaf_ = nullptr;
 int index_ = 0;
大致思路也很简单：

保存当前节点及当前index，++的时候只要判断是否到下个节点，如果到了下个点，将index置0；否则index++即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
INDEX_TEMPLATE_ARGUMENTS
auto INDEXITERATOR_TYPE::operator++() -> INDEXITERATOR_TYPE & {
  if (index_ == leaf_->GetSize() - 1 && leaf_->GetNextPageId() != INVALID_PAGE_ID) {
    auto next_page = buffer_pool_manager_->FetchPage(leaf_->GetNextPageId());
    next_page->RLatch();
    page_->RUnlatch();
    buffer_pool_manager_->UnpinPage(page_->GetPageId(), false);
    page_ = next_page;
    leaf_ = reinterpret_cast<LeafPage *>(page_->GetData());
    index_ = 0;
  } else {
    index_++;
  }
  return *this;
}

至于begin()和end()的实现，调用前面的FindLeaf()即可，此处不多追述了。

至此checkpoint1通关。

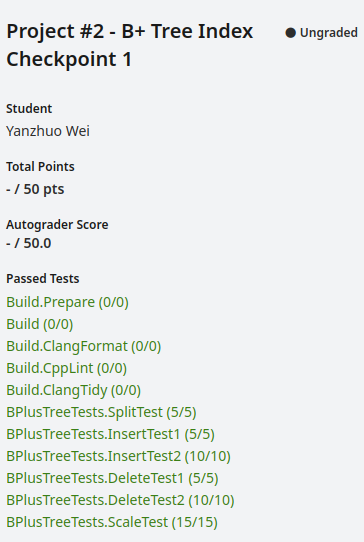
CheckPoint1搞定！！

Concurrent Index

课程中说了你一把大锁是肯定过不了我们的测试滴，所以我就没有尝试了，直接开始研究实现latch crabbing的方法了。

基本思想： 先锁住 parent page， 再锁住 child page。假设 child page 是安全的，则释放 parent page 的锁。

安全指当前 page 在当前操作下一定不会发生 split/steal/merge。

同时，安全对不同操作的定义是不同的。

Search 时，任何节点都安全；Insert 时，判断 MaxSize；Delete 时，判断 MinSize。

写到这里可以看到，FindLeaf()的实现是非常重要的。这里贴上安全判断、加锁及释放的操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
if (operation == Operation::SEARCH) {
  child_page->RLatch();
  page->RUnlatch();
  buffer_pool_manager_->UnpinPage(page->GetPageId(), false);
} else if (operation == Operation::INSERT) {
  child_page->WLatch();
  transaction->AddIntoPageSet(page);

  // child node is safe, release all locks on ancestors
  if (child_node->IsLeafPage() && child_node->GetSize() < child_node->GetMaxSize() - 1) {
    ReleaseLatchFromQueue(transaction);
    }
    if (!child_node->IsLeafPage() && child_node->GetSize() < child_node->GetMaxSize()) {
    ReleaseLatchFromQueue(transaction);
  }
} else if (operation == Operation::DELETE) {
  child_page->WLatch();
  transaction->AddIntoPageSet(page);

  // child node is safe, release all locks on ancestors
  if (child_node->GetSize() > child_node->GetMinSize()) {
    ReleaseLatchFromQueue(transaction);
  }
}

Insert

Insert操作中，需要进行的锁操作有： 1. 最开始的根节点的写锁，并且将nullptr加入transaction。（这是我的实现方法，在释放队列中个节点锁的时候进行判断，如果是空指针则unlock根节点锁） 

1
2
root_page_id_latch_.WLock();
transaction->AddIntoPageSet(nullptr);
对应的释放写锁的函数如下。

需要注意几个问题：

  • 先解锁再unpin！！因为 Unpin 后这个 page 的 pin_count 可能降为 0，buffer_pool_manager 可能会将该 Page 指针的内容改写为另一个 Page 的，导致 Unlock 错误。

  • 如果是nullptr则释放root_page_id_latch_的写锁。

1
2
3
4
5
6
7
8
9
10
11
12
13
INDEX_TEMPLATE_ARGUMENTS
void BPLUSTREE_TYPE::ReleaseLatchFromQueue(Transaction *transaction) {
  while (!transaction->GetPageSet()->empty()) {
    Page *page = transaction->GetPageSet()->front();
    transaction->GetPageSet()->pop_front();
    if (page == nullptr) {
      this->root_page_id_latch_.WUnlock();
    } else {
      page->WUnlatch();
      buffer_pool_manager_->UnpinPage(page->GetPageId(), false);
    }
  }
}

  1. 在return之前，解除FindLeaf()找到的page的写锁，leaf_page->WUnlatch();

  2. 使用ReleaseLatchFromQueue的时机。此处列举几处：

  • StartNewTree()之后，主要是为了释放 root_page_id_latch_；

  • 遇到重复的key或者无需进行分裂操作，return之前。

  • InsertIntoParent中，无需继续递归，直接return的时候。

其实就是Insert()操作彻底完成的时候。

  1. 释放锁的顺序问题。transaction 就是 Bustub 里的事务。释放锁的顺序可以从上到下也可以从下到上，但由于上层节点的竞争一般更加激烈，所以最好是 从上到下 地释放锁。这样可以获取更好的性能。

Remove

  1. 最开始的根节点的写锁，并且将nullptr加入transaction。(跟Insert类似)
  2. 无需合并或借item，或者调用coalesceOrRedistribute()之后，leaf_page->WUnlatch();(跟Insert类似)
  3. 使用ReleaseLatchFromQueue的时机。(跟Insert类似)
  4. 说些不同的，就是sibling_page->WLatch();找到兄弟节点之后要及时对他加锁。在对父节点解锁并unpin完毕后方可对sibling_page进行解锁。

另外，unpin一定要好好检查，并发测试出现的很多错误都是unpin操作不正确。

最后要记得delete掉所有需要delete的page。

coalesceOrRedistribute()的返回值是表明本page是否需要被delete。调用出来的时候需要进行一次判断。

1
2
3
std::for_each(transaction->GetDeletedPageSet()->begin(), transaction->GetDeletedPageSet()->end(),
                [&bpm = buffer_pool_manager_](const page_id_t page_id) { bpm->DeletePage(page_id); });
  transaction->GetDeletedPageSet()->clear();

遇到问题及解决方法

  1. InsertTest1中结果非常离谱。 

    1
    2
    3
    4
    Expected equality of these values:
    root_as_leaf->GetSize()
    Which is: 27504
    1
    这个Size()的错误一看就不像是对size_的错误操作造成的。查看测试代码文件，发现未补全GetRootPageId()函数。补全后错误解决。

  2. InsertTest2中有结果不正确 

    1
    2
    3
    4
    5
    Expected equality of these values:
      rids[0].GetSlotNum()
        Which is: 5
      value
        Which is: 4
    检查逻辑发现InsertIntoParent()的边界条件判断中if(parent_node->GetSize() == parent_node->GetMaxSize())应当改为if(parent_node->GetSize() == parent_node->GetMaxSize()-1)，这是因为parent_node一定是Internal page，而Internal page的第一个key是空出来而不计入size的。

  3. InsertTest3中结果有问题，GetValue()始终得到5. 

    1
    2
    3
    4
    5
    Expected equality of these values:
      rids[0].GetSlotNum()
        Which is: 5
      value
        Which is: 4

到这一步的时候我才使用项目提供的b_plus_tree_printer查看树的形状，发现乱七八糟的，于是查找原因，想起来忘记在intenal page分裂并且转移元素后改变子结点的parentid。 在MoveHalfTo()加入以下步骤，完善建树逻辑。

1
2
3
4
5
6
7
8
9
for (int i = 0; i < recipent->GetSize(); ++i) {
  auto child_page = buffer_pool_manager->FetchPage(recipent->ValueAt(i));
  BPlusTreePage* child_node = reinterpret_cast<BPlusTreePage*>(child_page->GetData());
  assert(child_node != nullptr);
  if (child_node->GetParentPageId() != recipent_page_id) {
    child_node->SetParentPageId(recipent_page_id);
    buffer_pool_manager->UnpinPage(child_node->GetPageId(), true);
  }
}

可在这之后还是有问题，就是倒序插入元素时，发现后几个数都是相同的。很容易就想到应该是在叶子页面的Insert()步骤中出错了。错误真的是有些蠢，就是插入元素在前面的时候，需要把后面的元素移到后面去为它腾出位置，此时应该从后往前遍历，而我从前往后遍历导致pos后面那家伙把剩下的全部覆盖掉了，就是一个初学c第一次写insert可能会犯的愚蠢错误....

  1. InsertTest3卡住了，应该是关于迭代器实现的问题。

    排查循环的问题，只有在end()的实现中存在循环。循环条件没毛病while (leaf->GetNextPageId() != INVALID_PAGE_ID)，但我想leaf page的nextpageid的处理，中间的node肯定都没有什么问题，最后的那个怎么办呢？此时答案就显而易见了，忘记初始化成INVALID_PAGE_ID了...

  2. DeleteTest中，删除操作不正确，好像有少删的情况，因为实际删除后的size比expected size大。

    使用可视化工具排查问题时，提示 

    1
    2
    Warning: COLSPAN value cannot be 0 - ignored
    Warning: COLSPAN value cannot be 0 - ignored

先是脑补了一遍删除一个最左边节点然后其右边节点与其合并的过程，发现没有什么问题。接着去检查一些简单的方法，发现是internal page的 ValueIndex()方法出现错误。不仔细。

1
2
3
4
5
6
7
8
9
INDEX_TEMPLATE_ARGUMENTS
auto B_PLUS_TREE_INTERNAL_PAGE_TYPE::ValueIndex(const ValueType &value) -> int{
  for(int i = 0; i < GetSize(); ++i) {
    if(array_[i].second == value){
      return i;
    }
  }
  return GetSize();
}

正确代码如上，我的循环初始条件写成了i=1，因为想到这是internal page所以第一个元素没有key，可是拜托你这里找的是value啊喂！

  1. DeleteTest size还是偏大，可是利用可视化工具首先发现内部节点指向混乱，前去完善interal page 的 MoveFirstToEndOf()以及MoveLastToFrontOf()两个方法的逻辑。接着利用可视化工具进行测试没有发现任何问题但还是无法通过测试。于是查看测试代码逻辑，发现其调用GetValue()函数，而我调用KeyIndex()后缺少对得到的index的大小判断，加上后顺利通过本地测试！

至此checkpoint2通关。

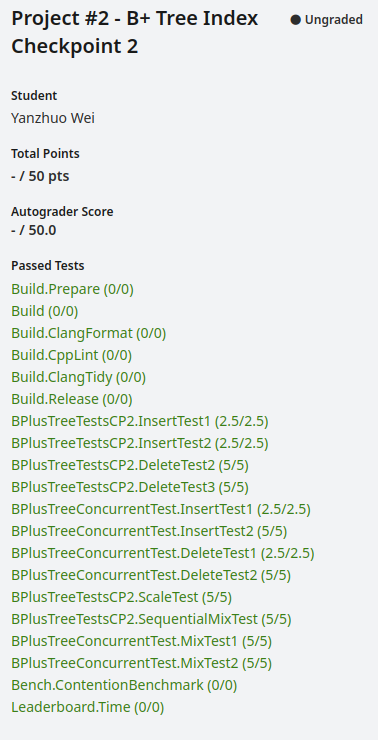
CheckPoint2搞定！！

最后leaderboard名次是34，还是有一定优化空间的。。。

B+树leaderboard
开发
#C++ #CMU15-445 #数据库
CMU15-445 PROJECT2 B+TREE INDEX 项目记录
http://example.com/2023/03/28/CMU15445-PROJ2/
作者
Melrose Wei
发布于
2023年3月28日
许可协议